5. Másodlagos adatbázisok

Alapfogalmak

• A másodlagos adatbázisok lényegében szekvenciamintázat-adatbázisok. Az elsődleges adatbázisokból (azaz a szekvenciaadatbázisokból) származtatják őket.
• Az elsődleges adatbázisokban lévő szekvenciák alapján többszörös szekvenciaösszerendezéseket készítünk. Ekkor láthatóvá válnak a konzerválódott régiók, a motívumok. A motívumok összességét nevezzük ujjlenyomatnak. Egy motívum alapján konstruálhatunk reguláris kifejezést, vagy gyakorisági mátrixot (ebből pedig súlyozott gyakorisági mátrixot).
  

  Másodlagos vagy harmadlagos adatbázis	Elsődleges vagy másodlagos forrása	Mit tartalmaz
  PROSITE	SWISSPROT	Reguláris kifejezések (mintázatok)
  Profiles (PROSITE része)	SWISSPROT	Súlyozott mátrixok (profilok)
  PRINTS	SWISSPROT+TrEMBL	Összerendezett motívumok (ujjlenyomatok)
  Pfam	SWISSPROT	Rejtett Markov modellek (HMM-ek)
  BLOCKS	PROSITE, ill. PRINTS	Összerendezett motívumok (blokkok)
  eMOTIF	BLOCKS, ill. PRINTS	"Fuzzy" reguláris kifejezések (mintázatok)

• A BLOCKS és az eMOTIF már harmadlagos adatbázisnak tekinthető, mert másodlagosból van származtatva.

Csoportosításuk

• Egy motívummal dolgozó adatbázisok: PROSITE (pontos reguláris kifejezésekkel dolgozik), eMOTIF (fuzzy reg. kif.)
• Több motívummal dolgozó adatbázisok: PRINTS (gyakorisági mátrixokkal készült) és BLOCKS (súlyozott gyakorisági mátrixokkal készült)
• Teljes összerendezésekkel dolgozó adatbázisok: Pfam (rejtett Markov-modellekkel), Profiles (a PROSITE másik része)

Mire jók?

• Bioinformatika alapfeladata: új szekvenciánál megállapítani a fehérje funkcióját, melyik fehérjecsaládba tartozik, stb.
• Keresőprogramok (FASTA, BLAST, PSI-BLAST, stb.) homológia felismerésére jók, de sokkal fontosabb az ortológia felismerése (a homológ lehet az ortológ paralógja is, ez kevésbé hasznosítható)
• Másodlagos adatbázisok az ortológia felismerését segítik: többnyire azonos funkciójú fehérjék szekvenciáiból származtatják őket.

Reguláris kifejezések: "aláírások" és "szabályok": PROSITE adatbázis

A PROSITE adatbázis tartalma: Reguláris kifejezések

Összerendezésből származtatható a reguláris kifejezés:

ADLGAVFALCDRYFQ
SDVGPRSCFCERFYQ
ADLGRTQNRCDRYYQ
ADIGQPHSLCERYFQ

[AS]-D-[IVL]-G-x4-{PG}-C-[DE]-R-[FY]2-Q

Jelölések

• A pozíciók között kötőjelek
• Egy aminosav-betűjel: teljesen konzerválódott pozíció (pl. -R-)
• Szögletes zárójelben: a megadott aminosavak valamelyike (pl. [IVL])
• Kapcsos zárójelben: Bármelyik aminosav, kivéve a megadottakat (pl. {PG})
• x: Bármelyik aminosav
• Szám: ismétlődés. (Pl. [FY]2, x4, x(2,4), stb.) x(2,4): x 2-ször, 3-szor vagy 4-szer.

PROSITE tartalma:

• Fehérjecsaládokra jellemző, azokat leíró reguláris kifejezések: "aláírások" (signatures)
• Egyéb, ismert funkciójú, gyakori mintázatokat megadó reguláris kifejezések: "szabályok" (rules). Pl.

  Hely	Szabály
  N-glikozilációs hely	N-{P}-[ST]-{P}
  Protein kináz C foszforilációs hely	[ST]-x-[RK]
  Kazein kináz II foszforilációs hely	[ST]-x(2)-[DE]
  Asp és Asn hidroxilációs hely	C-x-[DN]-x(4)-[FY]-x-C-x-C

• Profilok (ld. később)

A PROSITE készítése

• Manuálisan, szakértők által összeállított adatbázis
• Szakirodalomból összegyűjtik az egyes fehérjecsaládokra vonatkozó adatokat (funkció, aktív hely, kötőhelyek, fontos aminosavak, stb.)
• Kigyűjtik a fehérjecsalád tagjainak szekvenciáit a SWISSPROT-ból, többszörös összerendezést készítenek (automatikus + manuális igazítás)
• Szerkesztenek egy olyan reguláris kifejezést, amely nagy specificitással jellemzi a család tagjait (ált. aktív helyet vagy fontos szerkezeti elemet magában fogjaló szakasz). Ez általában egy, kiválasztott motívum alapján történik (egymotívumos módszer!)
• A SWISSPROT-on ellenőrzik a kifejezés jóságát (pozitív, téves pozitív, téves negatív, ill. részleges találatok számai)
• Részletes, alapos dokumentáció
• Kb. 1500 fehérjecsaládot foglal magába (2001 október), a növekedés lassú (munkaigényes)

PROSITE állományok

Háromféle:

• PROSITE mintázatállomány (példa)
  Tartalmazza a reguláris kifejezést, a család tagjainak felsorolását, a kifejezés jóságára vonatkozó adatokat (hány jó, hány fals találatot ad, stb.)
• PROSITE dokumentációs állomány (példa)
  Részletes leírást tartalmaz és megadja a reguláris kifejezést
• PROSITE profilállomány (ld. később)

Keresés a PROSITE-ban

• Kulcsszó, megnevezés, stb. szerint
• Új szekvenciában megtalálható-e valamely PROSITE reguláris kifejezés: ScanProsite. Opció: gyakori mintázatok (szabályok) kiszűrése. Példa
  Egyéb programok, szerverek is (pfscan, stb.)
• Adott reguláris kifejezés mit talál a SWISSPROT-ban: ScanProsite.

"Ujjlenyomatok": PRINTS

A PRINTS tartalma

Fehérjecsaládokra jellemző "ujjlenyomatok": összerendezések hézagmentes, konzerválódott szakaszainak ("motívumok") halmazai

A PRINTS készítése

• Kiinduló adatbázis: SWISSPROT+TrEMBL
• Egy fehérjecsalád néhány szekvenciáját kigyűjtik, manuálisan többszörös összerendezést készítenek
• Megállapítják a konzerválódott régiók helyét (leginkább vizuálisan), ezek a motívumok (kezdeti motívumhalmaz)
• Mindegyik motívumból gyakorisági mátrixot származtatnak. Pl.:

  Motívum:

  YVTVQHKKLRTPL YVTVQHKKLRTPL YVTVQHKKLRTPL AATMKFKKLRHPL AATMKFKKLRHPL YIFATTKSLRTPA VATLRYKKLRQPL YIFGGTKSLRTPA WVFSAAKSLRTPS WIFSTSKSLRTPS YLFSKTKSLQTPA YLFTKTKSLQTPA ^ ^ ^

  Gyakorisági mátrix:

  T C A G N S P F L Y H Q V K D E I W R M ---------------------------------------------------------- 0 0 2 0 0 0 0 0 0 7 0 0 1 0 0 0 0 2 0 0 0 0 3 0 0 0 0 0 2 0 0 0 4 0 0 0 3 0 0 0 6 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 3 0 0 1 0 0 0 3 0 0 0 0 0 0 2 2 0 1 1 0 0 0 0 0 0 0 3 0 4 0 0 0 0 1 0 4 0 1 0 0 1 0 2 0 1 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 10 0 9 0 0 0 0 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 0 0 2 0 0 6 0 0 0 0 0 0 0 0 0 0 0

  (A táblázat sorai az összerendezés oszlopainak felelnek meg.)

• A gyakorisági mátrix segítségével keresést végeznek a SWISSPROT+TrEMBL adatbázison.
  • Bármely szekvencia illeszkedése a motívumhoz pontozható a gyakorisági mátrix segítségével: a szekvencián végigmenve összeadjuk a mátrix megfelelő oszlopában (ami az adott aminosavnak megfelel) lévő gyakoriságokat
• A legjobb találatokat hozzáveszik és hozzárendezik a kezdeti motívumhoz, újabb gyakorisági mátrixot számítanak
• Az eljárást iteratívan ismétlik, amíg már nem lehet több szekvenciát hozzávenni a motívumhoz. Pl. a fenti mátrix 4 iteráció után:

  T C A G N S P F L Y H Q V K D E I W R M ---------------------------------------------------------- 0 0 4 0 0 0 0 8 4 34 0 0 15 0 0 0 1 7 0 0 0 4 15 0 0 0 0 0 7 0 0 0 37 0 0 0 10 0 0 0 50 0 0 0 0 3 0 18 0 0 0 0 0 0 0 0 0 0 0 2 3 0 12 2 1 8 0 3 6 0 0 0 14 0 0 0 15 2 0 7 9 2 2 2 1 1 0 0 0 0 1 25 0 20 0 6 0 0 4 0 14 0 2 0 0 4 0 14 0 8 31 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 70 0 0 0 0 2 0 0 0 2 1 0 17 0 0 0 0 0 0 0 52 0 0 0 0 1 0 0 0 0 0 0 0 0 0 73 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 68 0 44 0 0 0 0 6 0 0 0 0 12 11 0 0 0 0 0 0 0 0 0 0 1 0 0 0 69 0 0 0 3 0 0 0 0 0 0 0 0 0 2 0 11 0 0 7 0 0 53 0 0 0 0 0 0 0 0 0 0 0

• Az iterációk utáni motívumhalmaz diagnosztikus ereje nagyobb (jobban "diagnosztizálható" vele egy új szekvenciának az adott fehérjecsaláddal való homológiája).
• Kb. 1550 ujjlenyomatban kb. 9500 motívumot tartalmaz a PRINTS (2001 október)

PRINTS állományok

Példa

• Keresztreferenciák
• Irodalmi hivatkozások
• Dokumentáció (bőséges)
• Az ujjlenyomat diagnosztikus erejét mutató statisztikai adatok
• A valódi pozitív találatot adó fehérjék felsorolása
• Kezdeti (iteráció előtti) motívumkészletek (pozícióval és az előző motívumtól mért távolsággal)
• Végső (iterációk utáni) motívumkészletek

Keresés a PRINTS-ben

• Direkt hozzáférés: kulcsszó, leírás, stb. alapján
• Keresés szekvenciával: FingerPRINTScan: a motívumokból levezetett gyakorisági mátrixok segítségével
  • Az egyes motívumokra külön-külön keres, E értéket számol. Példakimenet Grafikus ábrázolást is ad, pl.
    
    
  • A grafikon vízszintes tengelyén a vizsgált szekvencia van, ezen mindegyik motívumot végigcsúsztatjuk, és kiszámítjuk a hasonlóságot a motívum és a szekvencia adott szakasza között, ezt tüntetjük fel. Mindegyik motívumra külön grafikon, a vizsgált szekvenciával való szignifikáns egyezések színezve vannak
  • Legbiztosabb: mindegyik motívummal szignifikáns egyezés, megfelelő sorrendben a szekvencia mentén
  • Nem szükséges mindegyik motívummal egyezés, részleges egyezés is informatív lehet, pl.:
    

"Blokkok": BLOCKS

A BLOCKS tartalma

Fehérjecsaládokra jellemző "blokkok" halmazai: összerendezések hézagmentes, konzerválódott szakaszainak halmazai (mint a PRINTS, de más az előállítási mód és az eredmény)

A BLOCKS készítése

• Kiindulás: a PROSITE-ban lévő fehérjecsaládok, azaz ezek szekvenciái
• Egy speciális algoritmus olyan régiókat keres, melyekben 3 konzerválódott aminosav található, pl.:

            SxxxxTxxxP
  	  SxxxxTxxxP
  	  ...

• Az így talált régiókat mindkét irányba kiterjeszti, amíg a hasonlóság megmarad, az esetleges átfedő régiókat összeolvasztja, stb. Bonyolult műveletek után végül marad egy hézagmentes, nem átfedő blokkokból álló halmaz, mely az összes szekvenciára jellemző
• A blokkokból súlyozott gyakorisági mátrixokat vezetnek le: a gyakorisági mátrix egy aminosavhasonlósági mátrixszal van súlyozva. Pl. a fenti PRINTS kezdeti mátrix a PAM250-nel súlyozva:

  T C A G N S P F L Y H Q V K D E I W R M ------------------------------------------------------------------------------- -29 -22 -29 -48 -24 -24 -46 40 -13 62 -10 -40 -22 -38 -44 -44 -15 16 -30 -22 -1 -32 -1 -18 -20 -10 -13 -9 20 -22 -21 -18 32 -23 -22 -20 32 -61 -26 19 0 -36 -18 -30 -24 -12 -30 36 0 24 -18 -36 -6 -30 -36 -30 6 -30 -18 -6 3 -29 3 -4 -10 -1 -7 -22 3 -31 -19 -15 14 -8 -15 -13 11 -52 -13 11 5 -48 -1 8 7 1 -4 -54 -31 -46 6 14 -17 27 6 5 -20 -48 18 -9 2 -27 -7 -19 -3 -5 -13 0 -16 6 8 -10 -11 -15 -13 -11 -7 -37 -4 -15 0 -60 -12 24 12 0 -12 -60 -36 -48 0 12 -24 60 0 0 -24 -36 36 0 6 -30 0 18 12 12 0 -48 -36 -42 -6 0 -18 30 0 0 -18 -30 18 -12 -24 -72 -24 -48 -36 -36 -36 24 72 -12 -24 -24 24 -36 -48 -36 24 -24 -36 48 8 -50 -20 -32 2 -2 0 -50 -34 -48 26 18 -24 32 -6 -6 -24 10 62 -2 24 -29 7 -5 5 6 0 -36 -24 -31 6 1 -6 1 4 4 -6 -56 14 -14 0 -36 12 -12 -12 12 72 -60 -36 -60 0 0 -12 -12 -12 -12 -24 -72 0 -24 -6 -44 -2 -18 -16 -10 -12 -10 22 -24 -18 -14 10 -22 -24 -18 6 -40 -26 16

  Bármely sorban az A aminosav súlyozott pontszáma:

  

  ahol G_X az X aminosav gyakorisága (a gyakorisági mátrix megfelelő sorából véve), D_XA az aminosavhasonlósági mátrixban az X és az A aminosavak hasonlóságának pontszáma, az összegzés során X mind a 20 lehetséges értéket felveszi. (Az A itt bármelyik aminosavat jelölheti.)

  A súlyozott mátrix engedékenyebb a súlyozatlan gyakorisági mátrixoknál: kevesebb azonosságot tartalmazó szekvenciákat is magasan pontoz.

  A gyakoriságok számításánál az egymással 80%-nál nagyobb azonosságot mutató szekvenciákat egy csoportba veszik és egy szekvenciaként veszik figyelembe, megfelelő súlyozó faktorokkal

  • Kalibrálás: A súlyozott gyakorisági mátrix segítségével pontozzák a SWISSPROT-ban lévő összes szekvenciát. A találatok csoportosítása:
    • Pozitív találatok: amelyek pontszáma egy meghatározott küszöbérték fölött van. Ezen belül:
      • Valódi pozitív találatok: tényleg az adott fehérjecsaládhoz tartoznak
      • Téves pozitív találatok: annak ellenére, hogy pontszámuk a küszöbérték fölött van, mégsem tartoznak az adott fehérjecsaládhoz.
    • Negatív találatok: amelyek pontszáma az említett küszöbérték alatt van. Ezen belül:
      • Valódi negatív találatok: tényleg nem tartoznak az adott fehérjecsaládhoz
      • Téves negatív találatok: annak ellenére, hogy pontszámuk a küszöbérték alatt van, mégiscsak az adott fehérjecsaládhoz tartoznak.

    (A fehérjecsaládhoz tartozónak azokat a szekvenciákat tekintik, amelyek a blokkok levezetéséhez felhasznált (PROSITE-ból vett) szekvenciák között vannak.)

  • A blokk diagnosztikus erejét három pontszámmal jellemzik:
    • Alsó kalibrációs pontszám: Az a pontszám, aminél a fehérjecsaládhoz nem tartozó szekvenciák (valódi negatívok + téves pozitívok) 99,5%-a kisebb pontszámot ad
    • Felső kalibrációs pontszám: A fehérjecsaládhoz tartozó szekvenciák (valódi pozitívok + téves negatívok) pontszámainak mediánja (a pontszámok fele fölötte van, fele alatta).
    • A blokk erőssége: A felső kalibrációs pontszám osztva az alsó kalibrációs pontszámmal és szorozva 1000-rel. Ez a blokk erőssége (strength): annak mértéke, mennyire képes a blokk (tkp. a mátrixszal számított pontszám) szétválasztani a fehérjecsaládhoz tartozó és az ahhoz nem tartozó szekvenciákat. Minél nagyobb ez, annál nagyobb a blokk diagnosztikus ereje.
      
  • Egy új szekvenciát a következőképpen bírálhatunk el: a számított pontszámát elosztjuk az alsó kalibrációs pontszámmal és megszorozzuk 1000-rel, s az eredményt összevetjük a blokk erősségével.

BLOCKS állományok

• Bevezető információk
• Maguk a blokkok, megadva két pontszámot (99,5% [alsó kalibrációs pontszám] és strength [a blokk erőssége])
• Az egyes szekvenciák, kezdő pozícióval, üres sorral elválasztva a 80%-nál nagyobb azonosságú csoportok
• Mindegyik szekvencia után egy pontszám, amely a szekvenciának a többitől való távolságát mutatja (max. 100)

Keresés a BLOCKS-ban

• Kulcsszó, leírás, stb. szerint
• Egy szekvencia összehasonlítása a BLOCKS-szal (a súlyozott gyakorisági mátrix segítségével): Blocks Searcher. Kimenet: Példa. Egyező blokkokat mutatja, E értékkel.
• A talált blokkok ún. logó-ja (aminosavgyakoriságok betűméretre konvertálva) megjeleníthető, pl.:
  

A BLOCKS bővítései

Több más adatbázist konvertáltak BLOCKS formátumra, így ezekben együttesen lehet keresést végezni.

(Az ábrán szereplő számok régebbiek!)

Profilok: PROSITE, Pfam

Tartalmuk

A profilok összerendezett szekvenciákból származtatott, a teljes szekvenciát leíró matematikai objektumok. Két fajtájuk:

• Súlymátrixok: súlyozott gyakorisági mátrixok (mint a BLOCKS-nál), kiegészítve pozíciófüggő gap opening és gap extension penalty-kkel (azaz a mátrix soraiban 22 szám van: 20 aminosav és 2 gap penalty). A PROSITE-ban ilyennel írják le azokat a fehérjecsaládokat, amelyekre nem találnak jó reguláris kifejezést.
• Rejtett Markov-modellek (Hidden Markov Model, HMM): Olyan valószínűségi modell, amely szekvenciákat "generál": tkp. lineáris lánc, amely egyezés (Match, M), inszerció (I) és deléció (D) állapotokból áll, az ezek átmeneteit jellemző számadatokkal. Pl.:
  

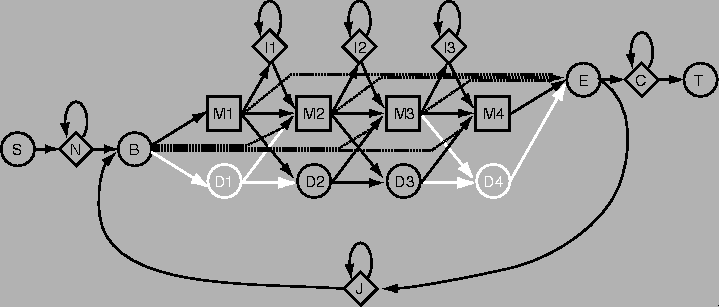
  A rejtett Markov-modell (angolul hidden Markov model, röviden HMM) egy képzeletbeli gép, amely szekvenciákat generál. A gépnek véges sok állapota van, és ezek között lépked. Minden egyes állapotában vagy minden egyes állapotváltáskor kibocsáthat egy szekvenciaelemet (tehát aminosavat vagy nukleotidot), ezekből áll össze a gép által generált szekvencia. A biológiai szekvenciák analíziséhez használt HMM-eknek alapvetően háromféle állapota van: M (match, azaz egyezés), I (insert, azaz inzerció) és D (delete, azaz deléció); ezeken kívül szokás még kiinduló- és végállapotokat és egyéb speciális állapotokat is definiálni. A fenti ábra egy HMM állapotdiagramját mutatja.

  A körök és a négyzetek a gép állapotait, az összekötő nyilak az egyes állapotok között lehetséges átmeneteket reprezentálják. Az M és az I állapotok ún. "kibocsátó" állapotok, tehát amikor a gép ezekben az állapotokban van, akkor kibocsát magából egy szekvenciaelemet (aminosavat vagy nukleotidot). A D állapotok nem kibocsátó állapotok. Mindegyik M és I állapothoz tartozik egy táblázat, amely megmondja, hogy az adott állapotban a 20 aminosav, ill. a 4 nukleotid közül melyiket milyen valószínűséggel bocsátja ki a gép (tehát a táblázat 20 vagy 4 számot tartalmaz). A HMM-nek további paraméterei az egyes állapotok közötti átmenetek valószínűségei, tehát az állapotdiagramon lévő, az egyes állapotokat összekötő nyilak mindegyikéhez tartozik egy valószínűségérték. A HMM rendszerint annyi M, I és D állapotot tartalmaz, amilyen hosszú szekvenciát tipikusan generál. A fenti ábrán látható HMM például 4 M állapotot tartalmaz, tehát amennyiben működése során nem megy át sem I, sem D állapoton és nem is kanyarodik vissza a J állapoton keresztül, akkor 4 aminosavból vagy nukleotidból álló szekvenciát generál.

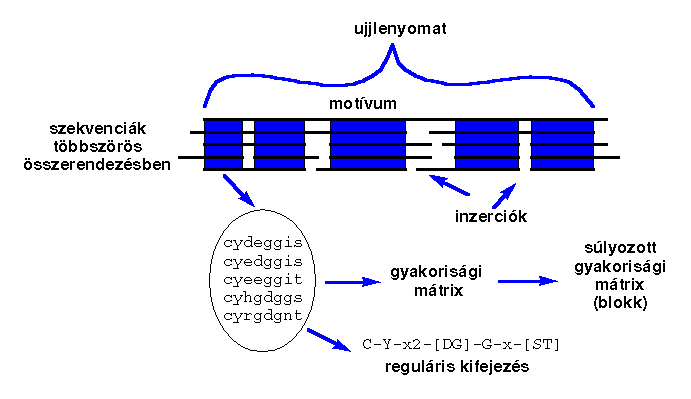
  Ha van egy szekvenciahalmazunk, amely egymással rokon szekvenciákat tartalmaz, akkor ennek a szekvenciahalmaznak az elemzésével, az egyes pozíciókban lévő aminosavak gyakorisága és más mennyiségek alapján definiálni lehet egy olyan HMM-et, amely olyan szekvenciákat generál, mint amilyenek a kiinduló szekvenciahalmazban vannak. A HMM felépítése, az állapotdiagram általában már eleve adott, a szekvenciahalmaz elemzésével pedig meghatározhatjuk az M és az I állapotokban az egyes aminosavak, ill. 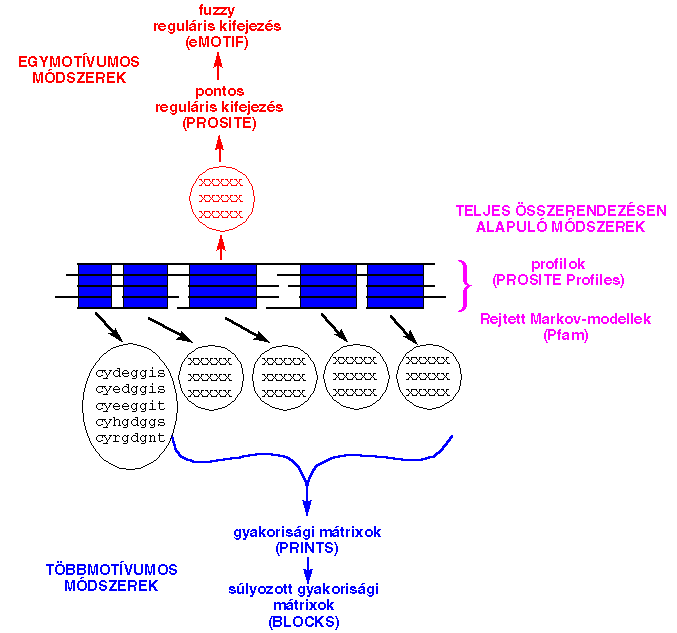nukleotidok kibocsátásának valószínűségeit, valamint a gép egyes állapotai közötti átmenetek valószínűségeit. A Pfam adatbázis ezeket a paramétereket (pontosabban a számítások megkönnyítése végett a valószínűségek logaritmusát) tartalmazza minden egyes fehérjecsaládra.

  Ha tehát a rokon szekvenciákat tartalmazó halmaz alapján definiáltunk egy HMM-et, akkor egy olyan modellünk van, amely ezt a bizonyos szekvenciacsaládot jól leírja, és képes további olyan szekvenciákat generálni, amelyek hasonlóak a kiinduló szekvenciahalmazban lévő szekvenciákhoz. A szekvenciaanalízisnél azonban a HMM-nek nem ez a képessége fontos, hanem egy másik tulajdonsága. Nevezetesen: a HMM segítségével meg lehet határozni egy új szekvenciáról, hogy azt milyen valószínűséggel generálhatja az adott HMM. Ha ez egy nagy valószínűségértéknek adódik, akkor állíthatjuk, hogy a vizsgált, új szekvencia is beletartozik abba a szekvenciacsaládba, amelyikből a HMM megkonstruálása során kiindultunk.

  Hogyan határozható meg egy új szekvenciáról, hogy mekkora valószínűséggel generálhatja azt egy bizonyos HMM? Egyszerű: meg kell nézni, hogy a HMM-nek mely állapotok egymásutánján kell végigmennie (vagyis az állapotdiagramban milyen útvonalat kell bejárnia) és mely állapotokban milyen szekvenciaelemet kell kibocsátania ahhoz, hogy éppen a vizsgált (új) szekvencia jöjjön ki. Ezután az állapotdiagramban bejárt útvonal mentén vett átmeneti valószínűségeket és a kibocsátó állapotokban a megfelelő szekvenciaelem kibocsátásának valószínűségeit összeszorozva adódik a vizsgált szekvencia generálásának teljes valószínűsége. (Általában több útvonal is vezethet ugyanahhoz a szekvenciához, ilyenkor vagy az összes lehetséges útvonal összegét, vagy a legvalószínűbb útvonalat szokás figyelembe venni.)

  A HMM-ek tehát olyan matematikai objektumok, amelyek szekvenciamintázatokat képesek leírni (legyenek azok akár nagyméretű fehérjeszekvenciák, akár néhány nukleotidból álló funkcionális helyek a DNS-ben). Új szekvenciák esetében segítségükkel egzakt valószínűségérték adható arra nézve, tartozhat-e az új szekvencia az adott HMM által leírt mintázatú szekvenciák csoportjába.

  A HMM-eket azért kedvelik, mert egzakt matematikai alapjuk van. Ugyanakkor vannak hátrányaik is. Szerkezetükból adódóan nem képesek megragadni például a szekvenciákban távolabb lévő aminosavak közötti korrelációkat (pl. korrelált mutációk esetében). További hátrány, hogy egy HMM által generált szekvencia egymástól független események egymásutánjának az eredményeként áll elő, ami a valóságban nincs így: a szomszédos szekvenciaelemekhez tartozó valószínűségértékek között a valóságban általában összefüggés van. A fehérjeszekvenciákban például a hidrofób aminosavak általában egymás mellé csoportosulnak, vagyis ha egy pozícióban hidrofób aminosav generálódott, akkor a következő pozícióban nagyobb valószínűséggel kellene szintén hidrofób aminosavnak generálódnia, mint egyébként, de ezt a HMM nem képes figyelembe venni. E tökéletlenségek ellenére a HMM-ek nagyon sikeresnek bizonyultak a szekvenciaanalízisben.

  A "rejtett Markov-modell" kifejezésben a "rejtett" jelző egyébként arra utal, hogy mi csak a modell működésének az eredményét, a kimenetet (azaz a generált szekvenciát) ismerjük, maga a modell és a paraméterei számunkra rejtettek. Tehát nekünk a kimenetből kell következtetnünk a modell felépítésére és a működését leíró paraméterekre (az átmeneti és a kibocsátási valószínűségekre).

  PROSITE-ban és Pfam-ban.

Elkészítésük

A többszörös összerendezésekből matematikai úton

PROSITE profilállomány

Példa

• Default paraméterek: különböző átmenetek (pl. MI: Match-Insertion) pontszámai
• M: Match (egyezés) állapotok, paraméterekkel (súlymátrix elemei)
• I: Inszerció állapotok, paraméterekkel

Pfam állományok

• Leíró állomány: Családok leírásai (szekvenciák felsorolása)
• HMM állomány: A HMM-et adja meg. Példa
• Pfam-A: Jól dokumentált családok, Pfam-B: rosszul dokumentált, automatikusan generált családok.

Keresés profiladatbázisokban

• Szekvencia összehasonlítása a profilokkal (különféle programok, szerverek)

"Fuzzy" reguláris kifejezések: eMOTIF

Az eMOTIF tartalma

Fuzzy reguláris kifejezések, különféle szignifikanciaszintekre optimalizálva.

Fuzzy: többféle aminosavat is megenged a konzerválódott pozíciókban, hasonlóság szerinti csoportokban:

ADLGAVFALCDRYFQ
SDVGPRSCFCERFYQ
ADLGRTQNRCDRYYQ
ADIGQPHSLCERYFQ

[ASGPT]-D-[IVLM]-G-x5-C-[DENQ]-R-[FYW]2-Q

Az engedékenység és a találatok számának viszonya:

Az eMOTIF készítése

• BLOCKS és PRINTS alapján kb. 270 000 fuzzy reguláris kifejezést kreáltak, különféle "engedékenységi" szintek mellett.

Keresés az eMOTIF-ban

• Csak szekvencia szerinti keresés végezhető, az eMOTIF programmal. Kimenet: Példa (BLOCKS és PRINTS találatok)

Integrált másodlagos adatbázis: INTERPRO

• A legjobban dokumentált másodlagos adatbázisok (PROSITE, PRINTS) integrálása egyéb másodlagos adatbázisokkal (Pfam, PRODOM, tervben a BLOCKS).
• Kb. 2850 fehérjecsalád (2001 október)

A másodlagos adatbázisok használata

Ld. példák