3. Páronkénti szekvencia-összerendezés

1. Alapfogalmak
2. Hasonlósági mátrixok (PAM, BLOSUM)
3. Statisztikai szignifikancia
4. A pontábrázolás
5. Lokális és globális hasonlóság
6. Globális összerendezés: Needleman--Wunsch-algoritmus
7. Lokális összerendezés: Smith--Waterman-algoritmus
8. Szekvenciahasonlósági keresések adatbázison (FASTA, BLAST)
9. Webhelyek

Alapfogalmak

Jelentőség

• Jelentősége: új, ismeretlen fehérjéhez tartozó szekvencia esetében az ismert szekvenciák adatbázisában kell keresni az újhoz hasonlókat.
• Meg kell állapítani a hasonlóság mértékét
• A nagy hasonlóság rokonságra utal, kis hasonlóság esetén a rokonság feltételes
• Rokonsági viszonyok fontosak. Pl. ha egy adott géncsaládnak az egérben 10 tagja van, az emberben pedig csak 7-et találtak, vsz. van még min. 3!
• A szekvencia-összerendezés a hasonlóság megállapításának eszköze

Ábécék, komplexitások

• Szekvencia: egy betűkészlet, ábécé elemeiből áll
• DNS: 4 betű, fehérje: 20 betű (néha még: X [ismeretlen], B [Asp/Asn], Z [Glu/Gln])
• EST: 5 betű (ATGC+N [ismeretlen])
• Programok az ismeretlen betűkkel sokféleképpen bánnak (felismeri/kicseréli/ figyelmen kívül hagyja/leáll, stb.)

Egyszerű manuális összerendezés

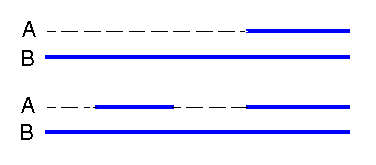
Összerendezés előtt:

                 1. szekvencia:      AGGVLIIQVG
		                     ||||||
		 2. szekvencia:      AGGVLIQVG

Összerendezés után:

                 1. szekvencia:      AGGVLIIQVG
		                     ||||| ||||
		 2. szekvencia:      AGGVL-IQVG

• Gap-et, hézagot szúrunk be, így az egyezések száma 6-ról 9-re nő
• Gyakorlatban hosszú, kevésbé hasonló szekvenciák
• Pontozni szükséges: egyezések és eltérések száma, beszúrt hézagok száma --> definiálható egy metrika, amely megadja két szekvencia távolságát
• Részszekvenciák:
  

Hasonlósági mátrixok

• Elvben 100%-os azonosságot érhetünk el az összerendezett pozíciókban, ha gátlástalanul hézagokat szúrunk be. Pl.:

  Q---ACFWE---MKVRT---ACFYI---MACP
  QMKV---WEACF---RTMKV---YIKVF---P
  

• Ennek azonban biológiailag nincs értelme. A hézagok beszúrását korlátozni kell: büntetőpontokat vezetünk be:
  • Gap opening penalty: új hézag beszúrásakor alkalmazott büntetőpont
  • Gap extension penalty: meglévő hézag növelésekor alkalmazott büntetőpont
• Értelmes összerendezésnél egymás alá kerülnek eltérő aminosavak is; nem mindegy, hogy mi mire cserélődik. Az aminosavak hasonlóságát pontozni kell. E pontszámokat tartalmazzák az aminosavhasonlósági mátrixok.
• Ha csak az azonosságokat vesszük figyelembe a pontozásnál, akkor egységmátrixot használunk:

  	A	C	G	T
  A	1	0	0	0
  C	0	1	0	0
  G	0	0	1	0
  T	0	0	0	1

  Egységmátrix nukleotidokra

  C S T P A G N D E Q H R K M I L V F Y W C 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 S 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 T 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 P 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 G 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 N 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 D 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 E 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 Q 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 H 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 R 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 K 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 M 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 I 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 L 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 V 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 F 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 Y 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 W 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

  Egységmátrix aminosavakra

  
  
• Ezek ún. ritka mátrixok. Hasonlósági keresésnél nem kedvezőek, mert csak a teljes egyezést veszik figyelembe, azokat is egyenlő súllyal.
• Szükség van "engedékenyebb" hasonlósági mátrixokra, amelyek a hasonló aminosavakat is jutalmazzák. Hátrány: növekszik a "zaj" is (hasonlósági keresésnél több találat adódik, nem rokon fehérjékkel is)
• A jel/zaj viszony a mátrixtól függ. Külön kutatási ág a jó aminosav-hasonlósági mátrixok megalkotása
• Hasonlósági mátrix alapján hasonlósági pontszám számítható az összerendezésre
• hasonlósági százalékérték: a pozitív hasonlósági pontszámú aminosavpárok százalékos aránya
• Sokféle mátrixot lehet definiálni, pl. az aminosavak fizikai-kémiai tulajdonságai alapján, vagy a mutációs gyakoriságok alapján.
• Két leggyakoribb mátrix: PAM és BLOSUM (mutációs gyakoriságok alapján definiált mátrixok).

A Dayhoff-féle PAM mátrixok

• 70-es években dolgozta ki Margaret Dayhoff és mtsai
• PAM = APM = Accepted Point Mutation (a szelekció által jóváhagyott mutáció)
• PAM: az evolúciós távolság mértékegysége is: 1 PAM az az evolúciós távolság (tkp. időtartam), amely két, kezdetben azonos szekvencia között 1% eltérést hoz létre pontmutációkkal.
• Dayhoff: a 70-es években ismert szekvenciák összehasonlításából aminosavcserék valószínűségét számította. Manuálisan összerendezett, >85% azonosságú szekvenciákból
• Számítható: XY aminosavcsere valószínűsége adott idő alatt (PAM-ban mérve), osztva az X és az Y aminosav gyakoriságával --> "relatedness odds matrix" (rokonsági esély mátrixa)
• Két szekvencia összehasonlításakor ezeket pozícióról pozícióra össze kéne szorozni. Egyszerűbb a logaritmusokat összeadni --> "log odds" mátrix

  Cisztein	C	12
  Speciális	S	0	2
  	T	-2	1	3
  	P	-3	1	0	6
  	A	-2	1	1	1	2
  	G	-3	1	0	-1	1	5
  Asx, Glx	N	-4	1	0	-1	0	0	2
  	D	-5	0	0	-1	0	1	2	4
  	E	-5	0	0	-1	0	0	1	3	4
  	Q	-5	-1	-1	0	0	-1	1	2	2	4
  Bázikus	H	-3	-1	-1	0	-1	-2	2	1	1	3	6
  	R	-4	0	1	0	-2	-3	0	-1	-1	1	2	6
  	K	-5	0	0	-1	-1	2	1	0	0	1	0	3	5
  Alifás	M	-5	-2	-1	-2	-1	-3	-2	-3	-2	-1	-2	0	0	6
  	I	-2	-1	0	-2	-1	-3	-2	-2	-2	-2	-2	-2	-2	2	5
  	L	-6	-3	-2	-3	-2	-4	-3	-4	-3	-2	-2	-3	-3	4	2	6
  	V	-2	-1	0	-1	0	-1	-2	-2	-2	-2	-2	-2	-2	2	4	2	4
  Aromás	F	-4	-3	-3	-5	-4	-5	-4	-6	-5	-5	-2	-4	-5	0	1	2	-1	9
  	Y	0	-3	-3	-5	-3	-5	-2	-4	-4	-4	0	-4	-4	-2	-1	-1	-2	7	10
  	W	-8	-2	-5	-6	-6	-7	-4	-7	-7	-5	-3	2	-3	-4	-5	-2	-6	0	0	17
  		C	S	T	P	A	G	N	D	E	Q	H	R	K	M	I	L	V	F	Y	W

  A log odds mátrix 250 PAM-ra. Pozitív értékek: konzervatív cserék, negatívak: valószínűtlen cserék. Az aminosavak tulajdonságaik szerint csoportosítva vannak felsorolva, ezért az átló közelében lévő pontszámok nagyobbak.

  
  
• 250 PAM: kb. 20% szekvenciaazonosságnak felel meg, ez a legérdekesebb tartomány, ezért a PAM250 mátrixot gyakran használják. (1 PAM idő alatt 1% eltérést okozó pontmutáció történik, 250-szer annyi idő alatt kb. 80%-nyi eltérést okozó pontmutáció).
• De: Elvben előre tudni kéne a szekvenciaazonosságot, és a megfelelő PAM mátrixot használni:

  A két szekvencia eltérése százalékban	Evolúciós távolság PAM-ban
  1	1
  10	11
  20	23
  30	38
  40	56
  50	80
  60	112
  70	159
  80	246

  
  (de a szekvenciaazonosság csak az összerendezés után számítható...)
• PAM mátrixok hátránya: a számokat >85% azonosságú szekvenciapárokból származtatták, ennél kisebb azonosságokra csak extrapolálták. Továbbá viszonylag kis számú szekvenciából származtatták az adatokat.

A BLOSUM mátrixok

• Henikoff és Henikoff 1992
• BLOCKS adatbázison alapul: ebben fehérjecsaládok többszörösen összerendezett szekvenciablokkjai vannak
• Szekvenciákból csoportokat, klasztereket képeznek a szekvenciahasonlóság alapján, pl. az egymással 62%-nál nagyobb azonosságot mutató szekvenciák egy klaszterbe kerülnek. Az azonosság mértéke alapján sokféle klaszter képezhető (80%, 60%, 40%, stb.)
• Aminosav-helyettesítési mátrixokat számolnak a klaszterekben lévő szekvenciák alapján --> BLOSUM 80, BLOSUM 60, BLOSUM 40, stb. mátrixok
• Gyakran használt: BLOSUM 62.
• Általánosságban biológiailag helyesebb összerendezéseket ad, mint a PAM mátrixok (ismert szerkezetű fehérjéknél ez ellenőrizhető).
• BLOSUM és PAM más-más aminosavcseréket részesít előnyben. Pl.:

  (a) Identities = 36/52 (69%), Positives = 47/52 (90%) Query: 214 KMGPGFTKALGHGVDLGHIYGDNLERQYQLRLFKDGKLKYQVLDGEMYPPSV 265 GP+FTK+ HGVDL+HIYG++LERQ +LRLFKDGK+KYQ+++GEMYPP+V Sbjct: 97 ERGPAFTKGKNHGVDLSHIYGESLERQHKLRLFKDGKMKYQMINGEMYPPTV 148 (b) Identities = 36/53 (68%), Positives = 47/53 (89%) Query: 214 KMGPGFTKALGHGVDLGHIYGDNLERQYQLRLFKDGKLKYQVLDGEMYPPSVE 266 + GP FTK HGVDL HIYG++LERQ++LRLFKDGK+KYQ+++GEMYPP+V+ Sbjct: 97 ERGPAFTKGKNHGVDLSHIYGESLERQHKLRLFKDGKMKYQMINGEMYPPTVK 149

  (a) PAM250 összerendezés, (b) BLOSUM 62 összerendezés. A preferált cseréket jelző + jelek nem ugyanott vannak, ezért a (b) összerendezés eggyel hosszabb is.

Statisztikai szignifikancia

• Bármely két szekvenciát össze lehet rendezni (elég engedékeny paraméterekkel), szemre még jó is lehet.
• Szükség van megbízhatósági mérőszámra
• A legtöbb program valamilyen statisztikai paramétert ad meg, pl.
  • P érték: annak a valószínűsége, h. a kapott összerendezés a véletlen szüleménye. Minél kisebb, annál jobb.
  • E érték: várható gyakoriság (expected frequency): adatbázison való kereséskor a véletlennek köszönhetően várható találatok száma. Pl. E=1 esetén 1 találat véletlenül is várható. Minél kisebb, annál jobb.

    Példa:

    >bbs|69040 70 kda cyclooxygenase-related protein [mice, Peptide Partial, 80aa] Score = 145 bits (362), Expect = 7e-34 Identities = 66/80 (82%), Positives = 73/80 (90%) Query: 294 LPGLMLYATLWLREHNRVCDLLKAEHPTWGDEQLFQTTRLILIGETIKIVIEEYVQQLSG 353 +PLGM+YAT+WLREHNRVCDLLK EHP WGDEQLFQT+RLILIGETIKIVIE+YVQ LSG Sbjct: 1 VPGLMMYATIWLREHNRVCDLLKQEHPEWGDEQLFQTSRLILIGETIKIVIEDYVQHLSG 60 Query: 354 YFLQLKFDPELLFGVQFQYR 373 Y +LKFDPELLF QFQY+ Sbjct: 61 YHFKLKFDPELLFNQQFQYQ 80

A pontábrázolás (dotplot)

• Két szekvencia összehasonlításának legegyszerűbb eszköze
• Téglalap alakú mátrix két tengelyére a két szekvencia
• Aminosavak/nukleotidok egyezése/hasonlósága esetén a megfelelő helyre egy pontot (X-et, stb.) teszünk

  M T F R D L L S V S F E G P R P D S S A G G M X T X F X X R X X D X X L X X L X X S X X X X V X S X X X X F X X E X G X X X P X X R X X P X X O S X X X X S X X X X A X G X X X G X X X

• Diagonális vonalak hosszabb egyező szakaszokat jelentenek
• Jel és zaj vizuálisan jól elkülöníthető
• Hosszabb szekvenciák:

  Két azonos szekvencia (sertés lizozim):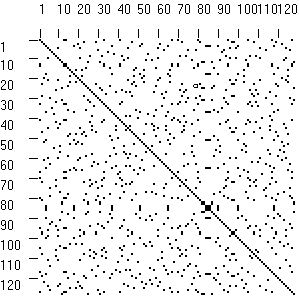
  Nagyon hasonló szekvenciák (rokon fajok lizozimjei):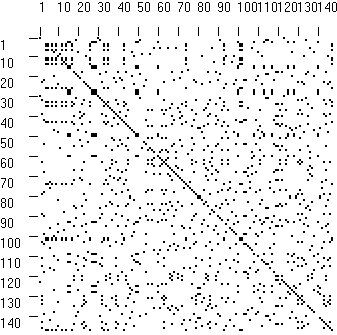
  Távoli, de rokon szekvenciák (lizozim és alfa-laktalbumin):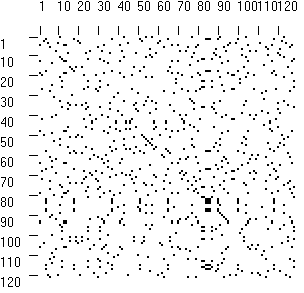

  
  
• Moduláris fehérjéknél a modulok azonosításának fontos eszköze
• Hasonlósági mátrixok alapján árnyalni, színezni is lehet, de a zaj nő.

Lokális és globális hasonlóság

• Globális hasonlóság: a szekvencia teljes hossza mentén
• Lokális hasonlóság: csak egyes régiókban
• Hasonlósági kereséseknél a lokális hasonlóságot célszerű keresni (funkció szempontjából fontos helyek gyakran rövid szakaszok, lokális keresés gyorsabb is)
• Nincs jó és rossz összerendezés, csak különböző matematikai modellek, melyek más-más biológiai szempontokra készültek

Globális összerendezés: Needleman--Wunsch-algoritmus

• Needleman & Wunsch 1970, később finomítások
• A két szekvencia maximális egyezését keressük, lehetséges deléciókkal. Gap penalty érvényben van.
• Szemléltetés: Rendezzük össze az ADLGAVFALCDRYFQ és az ADLGRTQNCDRYYQ szekvenciákat!
• A dotplotból kiindulva felírunk egy mátrixot, az egyezéseknél 1-eseket, az eltéréseknél 0-t írunk be, vagyis a H_i,j=s(a_i, b_j) képletet alkalmazzuk, ahol s(a_i, b_j) az a_i és b_j aminosavak hasonlósági pontszáma (itt az egységmátrixot alkalmazzuk):

  	A	D	L	G	A	V	F	A	L	C	D	R	Y	F	Q
  A	1	0	0	0	1	0	0	1	0	0	0	0	0	0	0
  D	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0
  L	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0
  G	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0
  R	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0
  T	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
  Q	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1
  N	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
  C	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0
  D	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0
  R	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0
  Y	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0
  Y	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0
  Q	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1

• Ezután a jobb alsó sarokból indulva, jobbról balra és lentről felfelé haladva kitöltjük a mátrixot a következő, rekurzív képlet szerint:
  H_i,j = H_i,j + max { H_i+1,j+1; max_k>=1 (H_i+k+1,j+1-W_k); max_k>=1 (H_i+1,j+k+1-W_k) }

  (Itt W_k a k hosszúságú hézaghoz tartozó gap penalty.)

  Tehát mindegyik cella tartalmához hozzáadjuk három érték közül a legnagyobbat. A három érték:

  1. a cellától jobbra és lefelé eső cella tartalma
  2. az eggyel lejjebb lévő sorban és legalább kettővel jobbrább lévő oszlopban oszlopban lévő elemek gap penaltyvel csökkentett értékeinek maximuma
  3. az eggyel jobbrább lévő oszlopban és legalább kettővel lejjebb lévő sorban lévő elemek gap penaltyvel csökkentett értékeinek maximuma

  W_k=0 gap penaltyt használva a mátrix félig kitöltve így fest:

  	A	D	L	G	A	V	F	A	L	C	D	R	Y	F	Q
  A	1	0	0	0	1	0	0	1	0	4	3	2	1	1	0
  D	0	1	0	0	0	0	0	0	0	4	4	2	1	1	0
  L	0	0	1	0	0	0	0	0	1	4	3	2	1	1	0
  G	0	0	0	1	0	0	0	0	5	4	3	2	1	1	0
  R	0	0	0	0	0	0	0	0	5	4	3	3	1	1	0
  T	0	0	0	0	0	0	0	0	5	4	3	2	1	1	0
  Q	0	0	0	0	0	0	0	0	5	4	3	2	1	1	1
  N	0	0	0	0	0	0	0	0	5	4	3	2	1	1	0
  C	0	0	0	0	0	0	0	0	4	5	3	2	1	1	0
  D	0	1	0	0	0	0	0	0	3	3	4	2	1	1	0
  R	0	0	0	0	0	0	0	0	2	2	2	3	1	1	0
  Y	0	0	0	0	0	0	0	0	2	2	2	2	2	1	0
  Y	0	0	0	0	0	0	0	0	1	1	1	1	2	1	0
  Q	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1

  A megjelölt 1-eshez hozzáadjuk az almátrix maximumát (5), így a cellába 6-os kerül.

  
  
• Az algoritmus értelme: a H_i,j mátrixelem az a_i és b_j aminosavpárral kezdődő és a két szekvencia végéig tartó legjobb lehetséges összerendezés pontszámát tartalmazza.
• Valamelyik N-terminálishoz érve készen van a mátrix. Az összerendezés visszafelé, a bal felső sarokból a jobb alsó felé haladva a maximális pontszámokat követve (backtracking) adódik:

  	A	D	L	G	A	V	F	A	L	C	D	R	Y	F	Q
  A	9	7	6	6	7	6	6	7	5	4	3	2	1	1	0
  D	7	8	6	6	6	6	6	6	5	4	4	2	1	1	0
  L	6	6	7	5	5	5	5	5	6	4	3	2	1	1	0
  G	5	5	5	6	5	5	5	5	5	4	3	2	1	1	0
  R	5	5	5	5	5	5	5	5	5	4	3	3	1	1	0
  T	5	5	5	5	5	5	5	5	5	4	3	2	1	1	0
  Q	5	5	5	5	5	5	5	5	5	4	3	2	1	1	1
  N	5	5	5	5	5	5	5	5	5	4	3	2	1	1	0
  C	4	4	4	4	4	4	4	4	4	5	3	2	1	1	0
  D	3	4	3	3	3	3	3	3	3	3	4	2	1	1	0
  R	2	2	2	2	2	2	2	2	2	2	2	3	1	1	0
  Y	2	2	2	2	2	2	2	2	2	2	2	2	2	1	0
  Y	1	1	1	1	1	1	1	1	1	1	1	1	2	1	0
  Q	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1

  Az útvonalat "leolvasva" adódik az összerendezés:

  ADLGAVFALCDRYFQ |||| |||| | ADLGRTQN-CDRYYQ

• (Megjegyzés: ebben a szemléltető példában az egyszerű pontozási rendszer (egységmátrix) és a gap penalty-k használatának mellőzése miatt a fenti mátrixból nem következik egyértelműen a megadott összerendezés).
• Ugyanezt gap penaltykkel, egységmátrix helyett pedig megfelelő hasonlósági mátrixokkal (PAM, BLOSUM), stb. alkalmazva: jó, optimális összrendezések (maximális pontszám a hasonlóságokat és a gap penaltyket figyelembe véve) nyerhetők.

Lokális összerendezés: Smith--Waterman-algoritmus

• Smith és Waterman 1981, később finomítások
• Hasonló a Needleman--Wunsch algoritmushoz, de rövid, lokálisan hasonló régiókat is megtalál. Két fő eltérés:
  1. A különböző (ill. nem hasonló) aminosavak párosítását negatív pontszámmal kell pontozni (és nem nullával)
  2. A mátrix kitöltésénél negatív értéket nem engedünk meg; ha negatív érték jönne ki, helyette 0-t írunk be.
• A mátrix mindegyik cellája egy lehetséges lokális összerendezés végpontja (jobb szélső eleme), az ehhez tartozó maximális hasonlósági pontszámot írjuk a cellába
  Szemléltetés: az előbb látott két szekvenciát rendezzük össze
• A mátrix éleit nullákkal töltjük fel (ezek nem lehetnek összerendezés végpontjai)

  	x	A	D	L	G	A	V	F	A	L	C	D	R	Y	F	Q
  x	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
  A	0.0
  D	0.0
  L	0.0
  G	0.0
  R	0.0
  T	0.0
  Q	0.0
  N	0.0
  C	0.0
  D	0.0
  R	0.0
  Y	0.0
  Y	0.0
  Q	0.0

• A bal felső sarokból indulva balról jobbra és fentről lefelé haladva a mátrixot feltöltjük pontszámokkal. Az (i,j) cellába írandó pontszámot a következő rekurzív képlet szerint számítjuk:

  H_i,j = max { H_i-1,j-1 + s( a_i, b_j);    max_k>=1 ( H_i-k,j - W_k );     max_k>=1 ( H_i,j-k - W_k );    0 }

  Tehát kiszámítunk 3 értéket, jelentésük: az (i,j) cellánál végződő lokális összerendezés pontszáma 3 lehetséges esetben:

  1. Az a_i és b_j aminosavak az összerendezésben egymásnak meg vannak feleltetve. Pontozása: Az aminosavpár hasonlósági pontszámához (s(a_i,b_j)) hozzáadjuk az (i-1,j-1) cellában lévő pontszámot (H_i-1,j-1), ez az eggyel rövidebb összerendezés pontszáma). A mátrix ezekkel a számokkal kitöltve így fest:

     	x	A	D	L	G	A	V	F	A	L	C	D	R	Y	F	Q
     x	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
     A	0.0	1.0	0.0	0.0	0.0	1.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
     D	0.0	0.0	2.0	0.0	0.0	0.0	0.7	0.0	0.0	0.7	0.0	1.0	0.0	0.0	0.0	0.0
     L	0.0	0.0	0.0	3.0	0.0	0.0	0.0	0.3	0.0	1.0	0.3	0.0	0.7	0.0	0.0	0.0
     G	0.0	0.0	0.0	0.0	4.0	0.0	0.0	0.0	0.0	0.0	0.7	0.0	0.0	0.3	0.0	0.0
     R	0.0	0.0	0.0	0.0	0.0	3.7	0.0	0.0	0.0	0.0	0.0	0.3	1.0	0.0	0.0	0.0
     T	0.0	0.0	0.0	0.0	0.0	0.0	3.3	0.0	0.0	0.0	0.0	0.0	0.0	0.7	0.0	0.0
     Q	0.0	0.0	0.0	0.0	0.0	0.0	0.0	3.0	0.0	0.0	0.0	0.0	0.0	0.0	0.3	1.0
     N	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	2.7	0.0	0.0	0.0	0.0	0.0	0.0	0.0
     C	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	2.3	1.0	0.0	0.0	0.0	0.0	0.0
     D	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	2.0	2.0	0.0	0.0	0.0	0.0
     R	0.0	0.0	0.0	0.7	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.7	3.0	0.0	0.0	0.0
     Y	0.0	0.0	0.0	0.0	0.3	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.3	4.0	0.0	0.0
     Y	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	2.3	3.7	0.0
     Q	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	2.0	4.7

     A mátrix a H_i,j = max { H_i-1,j-1 + s( a_i, b_j); 0} képlet szerint kitöltve. Egyezés pontszáma 1, eltérésé -1/3. Egy tizedesre kerekített értékeket adtunk meg.

     
     
  2. Az a_i aminosav egy k hosszúságú deléció végén helyezkedik el (k darab hézag van előtte). Pontozása: a deléciót megelőző utolsó összerendezett aminosavpár pontszáma (H_i-k,j), mínusz a k darab delécióhoz tartozó gap penalty, W_k. Ezt az összes lehetséges k-ra végig kell próbálni és a maximális pontszámot kell venni.
  3. A b_j aminosav egy k hosszúságú deléció végén helyezkedik el (k darab hézag van előtte). Pontozása: a deléciót megelőző utolsó összerendezett aminosavpár pontszáma (H_i,j-k), mínusz a k darab delécióhoz tartozó gap penalty, W_k. Ezt az összes lehetséges k-ra végig kell próbálni és a maximális pontszámot kell venni.
• E 3 érték maximumát írjuk a cellába, illetve ha ez negatív, akkor nullát, hogy a rossz lokális összerendezések ne éreztessék a hatásukat a szomszédos szegmenseknél.

  Végeredmény:

  	x	A	D	L	G	A	V	F	A	L	C	D	R	Y	F	Q
  x	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
  A	0.0	1.0	0.0	0.0	0.0	1.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
  D	0.0	0.0	2.0	0.7	0.3	0.0	0.7	0.0	0.0	0.7	0.0	1.0	0.0	0.0	0.0	0.0
  L	0.0	0.0	0.7	3.0	1.7	1.3	1.0	0.7	0.3	1.0	0.3	0.0	0.7	0.0	0.0	0.0
  G	0.0	0.0	0.3	1.7	4.0	2.7	2.3	2.0	1.7	1.3	1.0	0.7	0.3	0.3	0.0	0.0
  R	0.0	0.0	0.0	1.3	2.7	3.7	2.3	2.0	1.7	1.3	1.0	0.7	1.0	0.0	0.0	0.0
  T	0.0	0.0	0.0	1.0	2.3	2.3	3.3	2.0	1.7	1.3	1.0	0.7	0.3	0.7	0.0	0.0
  Q	0.0	0.0	0.0	0.7	2.0	2.0	2.0	3.0	1.7	1.3	1.0	0.7	0.3	0.0	0.3	1.0
  N	0.0	0.0	0.0	0.3	1.7	1.7	1.7	1.7	2.7	1.3	1.0	0.7	0.3	0.0	0.0	0.0
  C	0.0	0.0	0.0	0.0	1.3	1.3	1.3	1.3	1.3	2.3	1.0	0.7	0.3	0.0	0.0	0.0
  D	0.0	0.0	1.0	0.0	1.0	1.0	1.0	1.0	1.0	1.0	2.0	2.0	0.7	0.3	0.0	0.0
  R	0.0	0.0	0.0	0.7	0.7	0.7	0.7	0.7	0.7	0.7	0.7	1.7	3.0	1.7	1.3	1.0
  Y	0.0	0.0	0.0	0.0	0.3	0.3	0.3	0.3	0.3	0.3	0.3	0.3	1.7	4.0	2.7	2.3
  Y	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.3	2.7	3.7	2.3
  Q	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	2.3	2.3	4.7

  A teljesen kitöltött mátrix. A k darab delécióhoz tartozó gap penalty értéke: W_k=1+(1/3)k volt. A megjelölt 1.7-es érték származtatása: az átlósan fölötte lévő érték 2.0, ehhez hozzáadva az eltérés pontszámát (-1/3) kapjuk az 1.7-et. Az elemmel azonos sorban és oszlopban lévő elemek közül a megjelölt 3.7 adja a maximumot, ebből a 3 delécióhoz tartozó gap penaltyt (1+3*(1/3)=2) levonva szintén 1.7-et kapunk, így a cellába 1.7 kerül.

  
  
• Az összerendezés származtatása: megkeressük az egész mátrixban a legnagyobb értéket, s ebből két irányba haladunk a maximális pontszámok mentén. Itt a jobb alsó sarokban lévő 4.7-től indulva:

  ADLGAVFALCDRYFQ ADLGRTQNC-DRYYQ

• A következő legjobb lokális összerendezés megkapható, ha megkeressük a második legnagyobb értéket a mátrixban, amely nem része az első összerendezésnek, s ebből haladunk két irányba, stb.
• A Needleman--Wunsch és Smith--Waterman algoritmusok a dinamikus programozásnak nevezett algoritmusok kategóriájába tartoznak (a probléma megoldását kisebb alproblémák megoldására vezeti vissza)
• A lokális és a globális összerendezés ebben az esetben nagyon hasonló eremdényt szolgáltatott. Ez nem mindig van így. Példa:

  Összerendezendő szekvenciák: TTGACACCCTCCCAATTGTA és ACCCCAGGCTTTACACAT Globális összerendezés: TTGACACCCTCC-CAATTGTA :: :: :: : ACCCCAGGCTTTACACAT--- Lokális összerendezés: ---------TTGACACCCTCCCAATTGTA TTGACAC :: :::: vagyis :: :::: ACCCCAGGCTTTACACAT----------- TTTACAC